크루스칼 알고리즘이란?
크루스칼 알고리즘(Kruskal algorithm) 또는 크러스컬 알고리즘(Kruskal's algorithm)은 모든 노드를 최소한의 비용으로 연결하는 알고리즘이다.
크루스컬 알고리즘은 최소 비용 신장 트리(Minimal Spanning Tree, MST)를 구하는 대표 알고리즘입니다.
신장 트리(Spanning Tree)는 기존 그래프의 모든 노드를 포함하지만 싸이클이 존재하지 않는 그래프 트리를 말합니다.


예를 들어 다음과 같은 그래프가 있습니다.

노드는 총 7개가 있고 노드를 연결하는 간선은 11개입니다.
크루스칼 알고리즘은 싸이클이 발생하지 않는다고 했습니다. 싸이클이 발생하는지 안 하는지 여부를 확인하기 위해서는 다음과 같은 과정이 필요합니다.
노드의 최종 부모를 가리키는 check배열이 있습니다. 각 노드는 현재 독립적으로 자기 자신이 최종 부모입니다. 즉, 1번 노드는 1의 값을 가지고 2번 노드는 2의 값을 가집니다. 나머지 노드들도 같습니다.
두 노드를 연결하면 둘 중 작은 값을 가집니다. 즉, 1번 노드와 2번 노드가 연결되면 check배열의 [2]는 1의 값을 가집니다.
이제 크루스칼 알고리즘의 동작 과정입니다.
크루스칼 알고리즘은 각 간선을 오름차순으로 정렬하는 것으로 시작합니다.
12(1, 7) //거리12인 1과 7을 연결하는 간선
20(4, 7)
21(2, 4)
23(1, 4)
26(1, 2)
29(3, 5)
30(5, 6)
36(2, 3)
37(3, 6)
45(2, 5)
55(3, 7)
1과 7을 연결하는 12의 비용을 가진 간선이 가장 작은 값을 가집니다. 1과 7을 연결합니다.
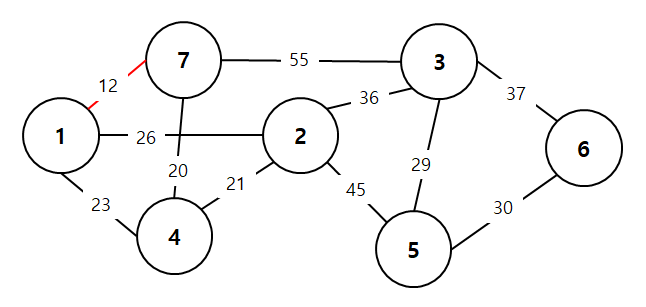
계속해서 연결해서 4와 7 그리고 2와 4까지 연결합니다.

12(1, 7) //연결
20(4, 7) //연결
21(2, 4) //연결
23(1, 4)
26(1, 2)
29(3, 5)
30(5, 6)
36(2, 3)
37(3, 6)
45(2, 5)
55(3, 7)
이제 1과 4를 연결할 차례입니다. 그러나 1과 4를 연결하면 싸이클이 발생합니다. 따라서 1과 4를 연결하는 간선은 연결하지 않습니다.
이러한 과정을 반복하게 되면 다음과 같이 연결되게 됩니다.

12 + 20 + 21 + 36 + 29 + 30 = 148의 비용으로 최소 비용 신장 트리를 구성했습니다.
#include <stdio.h>
#include <vector>
#include <algorithm>
using namespace std;
int check[7]; //노드 연결용, 연결노드가 바뀌는지 체크
class Edge{
public:
int node[2];
int distance;
Edge(int a, int b, int distance){
this->node[0] = a;
this->node[1] = b;
this->distance = distance;
}
//간선을 오름차순으로 정렬할때 기준을 distance로 정해줍니다.
bool operator<(Edge &edge){
return this->distance < edge.distance;
}
};
int getParent(int node){
if(check[node]==node) return node;
return getParent(check[node]);
}
//두 노드를 작은값을 기준으로 연결합니다.
void unionParent(int node1, int node2){
node1 = getParent(node1);
node2 = getParent(node2);
if(node1<node2) check[node2] = node1;
else check[node1] = node2;
}
//싸이클이 존재하면 true, 아니면 false를 반환
bool isCycle(int node1, int node2){
node1 = getParent(node1);
node2 = getParent(node2);
if(node1==node2) return true;
else return false;
}
int main(){
//두 노드를 연결할 간선을 정해줍니다.
vector<Edge> v;
v.push_back(Edge(1, 7, 12));
v.push_back(Edge(1, 4, 23));
v.push_back(Edge(1, 2, 26));
v.push_back(Edge(2, 3, 36));
v.push_back(Edge(2, 4, 21));
v.push_back(Edge(2, 5, 45));
v.push_back(Edge(3, 5, 29));
v.push_back(Edge(3, 6, 37));
v.push_back(Edge(3, 7, 55));
v.push_back(Edge(4, 7, 20));
v.push_back(Edge(5, 6, 30));
//간선을 오름차순으로 정렬합니다.
sort(v.begin(), v.end());
//각 노드는 자기자신이 부모로 초기화해줍니다.
for(int i=1;i<=7;++i){
check[i] = i;
}
int sum = 0;
for(int i=0;i<v.size();++i){
//싸이클이 존재하지 않으면 비용을 더합니다.
if(!isCycle(v[i].node[0], v[i].node[1])){
sum+=v[i].distance;
unionParent(v[i].node[0], v[i].node[1]);
}
}
printf("%d\n", sum);
return 0;
}
결과값:
148'알고리즘' 카테고리의 다른 글
| [C/C++] 코드업(codeup) 3011번 거품 정렬(Bubble Sort) (0) | 2020.01.19 |
|---|---|
| [C++] 코드업(codeup) 3004번 데이터 재정렬 (0) | 2020.01.18 |
| [C/C++] 깊이 우선 탐색(DFS) (0) | 2020.01.16 |
| [C/C++] 너비 우선 탐색(BFS) (0) | 2020.01.15 |
| [C/C++] 힙 정렬(heap sort)로 오름차순 정렬하기 (2) | 2020.01.12 |

